No.190　設計用地震力の分布を表す A_i の導き方

ちょっと真面目チョット皮肉 No. 190

石山祐二*

1981 年から用いられている日本の耐震規定（新耐震）では、上階ほど大きくなる設計用地震力（地震層せん断力係数）の分布を次の Ai で表している。

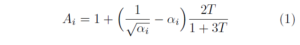
ここで、α_i は i 階の基準化重量、T は（高層になるほど大きくなる）建物の固有周期 (s) である。

A_i をグラフで示したのが図 1a) で、（T の値に応じて）複数の曲線（T = 0 の場合は直線）となっている。A_i に α_i を乗じると図 1b) の 1 階で 1 となる（基準化）地震層せん断力 Q_i/Q₁ = A_i α_i となる。

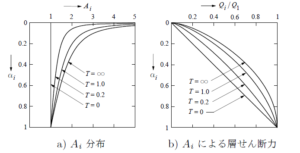
いずれも縦軸が α_i で、低層・超高層にかかわらず最上階で最小、1階で最大の 1.0（図 2）となる非常に便利なパラメータである。

 

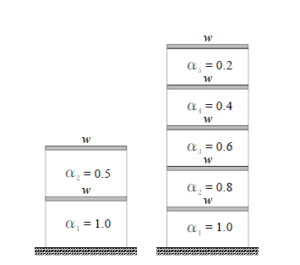
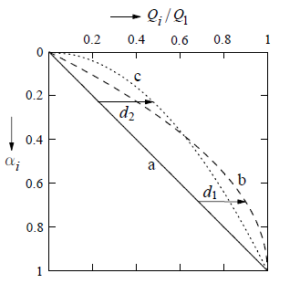
図 1b) は左上端から右下端を結ぶ上に膨らんだ複数の曲線からなっている。これらの曲線は図 3 の実線の直線 a（式で表すとα_i）、破線の（左に開いた）放物線 b（2α_i － α²_i ）、点線の（上に凸の）放物線 c (√α_i）を組合せたもので、放物線 b と直線 a の差を d₁、放物線 c と直線 a の差を d₂ とすると、これらの曲線は直線 aに k₁d₁ と k₂d₂ を加えたものとして次のように表すことができる。

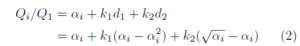
上式をα_i で除すと次の層せん断力係数が得られる。

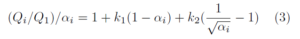
上式で k₁= k₂=2T/(1 + 3T) とすると(1) 式となる。

このようにして A_i を導いたが、（海外の耐震規定でよく用いられている）高さ h の代わりにα_i を用いていることには是非注目して欲しい。図 3 の直線 a（旧耐震で用いられていた建物の上階も下階も同様に揺れる「震度一様分布」）、曲線 b（世界各国で用いられている上階ほど直線的に大きく揺れる「震度逆三角分布」）、曲線 c（基礎固定一様せん断棒が基礎にホワイトノイズを受ける際の層せん断力の分布で超高層の鞭振り現象を表す「√α_i分布」）を容易に式で表すことができ、上に示したように式の誘導も容易になる。なお、超高層の鞭振り現象を表すため最上階に集中地震力（ニュージーランドの規定ではベースシヤの 8%）を加える規定もあるが、√α_i 分布の方が適用範囲が広い。しかし、α_iや√α_iを耐震規定に取り入れている国は日本のみである。

A_i の最後の 2T/(1 + 3T) については、T = 0 とするとこの値が 0 となるので A_i = 1.0（図 1a,b の直線と図 3 の直線 a）となり、T が大きくなると図3 の曲線 b と c の影響が徐々に大きくなる。T =∞では 2T/(1 + 3T)=2/3 となり、これは T がいくら大きくなっても中間階の地震層せん断力が最下階よりは大きくならないようにした結果である。

A_i は用いられてから 40 年以上も経過している。今振りかえると、(2) 式の表現はよいが k₁ = k₂ =2T/(1 + 3T) としたのは旧耐震に拘りすぎたかも知れない。2T/(1 + 3T) の中の 1 は必ずしも 1 である必要はなかったが、たまたま 1 として計算してみた結果、良さそうな式となり提案した次第である。最後に、T の代わりに地盤周期 T_c を用いて 0.6T/T_c としておけば（第 2 種地盤では A_i と同一になる）、もう少し洗練された式になったとも思っている

 

---

*いしやまゆうじ　北海道大学名誉教授
（一社）建築研究振興協会発行「建築の研究」2022.1 原稿