ちょっと真面目チョット皮肉 147
石山祐二 *
積雪によって柱と柱が数 10m も離れている大スパン構造物の崩壊は時々生じ、その原因として(1) 積雪が異常に多かった、(2) 雪が片寄って積もった、(3) 雨が降って雪が重くなったなどがある。しかし、他にも原因があるのではと思い、次のように考えてみた。
等分布荷重 w を受ける図 1 の構造物を図 2 のようにモデル化し、柱頭・梁(はり)端の曲げモーメントを M1、梁中央の曲げモーメントを MC とする。経済設計となるように M1 = MCとすると、これらの値は wℓ2/16(ℓ はスパン)となり、柱脚 A と D には反力 P1 = wℓ2/(16h)( h は高さ)が作用する。
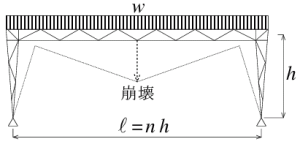

大スパン構造物には A~D 間に繋(つなぎ)梁が設けられていない場合が多いので、 P1 は基礎と地盤との摩擦力によって生ずるとする。 A と D の基礎に作用する鉛直力は wℓ/2 、摩擦係数を 0.5 とすると摩擦力は F = wℓ/4 となる。 ℓ = nh(高さの n 倍がスパン)とし、摩擦力と反力が等しいとすると n = 4 となる。
すなわち、 n が 4 を超えると図 2 の反力は摩擦力を超え、 n が更に大きくなると、梁の曲げモーメントは図 3 に近づく。結局、梁中央の曲げモーメントは図 2 の 2倍の M0 = wℓ2/8 となり、これが崩壊原因の一つに違いない。

更に、図 4 のように反力 P2 が逆向きに生ずると、柱頭・梁端に曲げモーメント M2= P2h が生じ、梁中央の曲げモーメントは MM = M0 + M2 となる。このような状態はめったに生じないと思うが、力が直接加わらなくとも、基礎が移動し柱脚 A~D 間が広がったり、あるいは(低温により)梁が縮み柱頭 B~C 間が短くなっても P2 が生ずる。
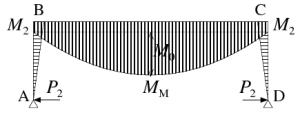
この影響を(計算の詳細は省略するが)次のように推察してみた。
梁の曲げ剛性を EI とし、柱は梁に比べて短いので剛と見なすと、 P2 によって柱脚 A~D 間は Δ = nh3 P2/(EI) 広がることになる。一方、図2 の梁中央の撓み
2wℓ4/(384EI) が撓み制限の ℓ/250 に等しいと仮定すると EI ≈ 1.3wℓ3 が得られる。よって、Δ ≈ nh3 P2/(1.3wℓ3) となる。ここで、 M2 が M1 に等しくなる場合を考えると、Δ ≈ h/20 となる。
すなわち、柱脚 A~D 間が h/20 広がると、 M2 = M1 = M0/2 となり、これも崩壊原因となる。もっとも、柱脚 A~D 間の広がりが h/20 となる(左右の柱が1/40 傾く)ことは通常は起こらないかも知れないが、高さ 5m・スパン 50m の場合には柱脚 A~D 間が 25cm広がることになり、地盤・地形状況によっては柱脚が基礎・地盤とともにこの程度移動することは考えられる。
次に、温度による影響を考えてみよう。鋼材の熱膨張率は 0.00001/度なので、温度変化を t 度とすると梁はΔ = tℓ/100000 伸縮する。真夏には直射日光によって鋼材は手で触ると火傷をするくらい高温になり、真冬には零下 30 度を下回ることもある。よって、 t を 50 度と仮定し、Δ = ℓ/2000 = nh/2000 から、n = 10 とすると
Δ = h/200 となる。すなわち、 M2 は M1 の1/10となり、この程度の温度変化のみでは崩壊を引き起こすことはないであろう。
以上の考察から、積雪による大スパン構造物崩壊の原因は、積雪が多かったことの他に、基礎を繋ぐ梁がないこと、そして十分な摩擦力が生じなかった、あるいは柱脚が広がるように基礎が移動したことが考えられる。対策として、剛強な繋梁を設けるか、設けない場合は図 3 の状態となることを想定した設計を行い、基礎が移動し難いように設計すするならば、この種の事故は大幅に防げると思っている。
* いしやまゆうじ 北海道大学名誉教授
(社団法人)建築研究振興協会発行「建築の研究」2013.4掲載