ちょっと真面目チョット皮肉 No. 186
石山祐二*
円周率 π は円周の長さと円の直径の比で、半径 r の直径は 2r なので円周の長さは次式となる。
| 円周の長さ:2πr | (1) |
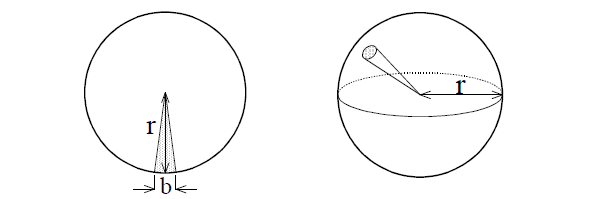
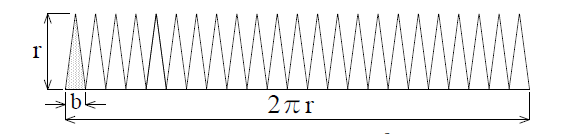
円の面積は図 1 左のように(ピザパイを多人数に分けるように)幅 b で高さ r の三角形に分割(正確には扇形となるが b を小さくすると三角形に近似)すると、この三角形の面積は 1/2br となる。円全体を細長い三角形に分割し、図 2 のように並べると底辺の長さの和は円周の長さの 2πrとなるので、三角形の面積の和 1/2×2πr×r となり、円の面積は次式で得られる。
| 円の面積:πr2 | (2) |
球に関する式を導くのは少し面倒で、(他の考え方もあるが)次のように考える 1)。図 3 左のような半径 r の半球について上から x の水平断面(円)について、この半径を y とするとピタゴラスの定理から x2 + y2 = r2 となるので、この円の面積 S1 は次式となる。
| 半球の切断面の面積:S1=πy2=π(r2–x2) | (3) |
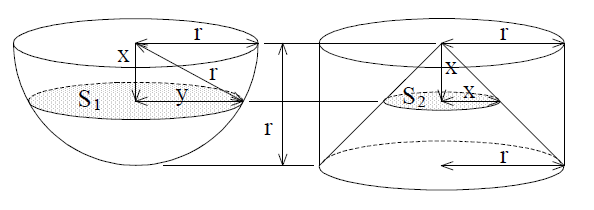
次に図 3 右のように底面の半径 r、高さ r の円錐について頂点から x の水平断面(円)を考えると、その半径も x なので、この円の面積 S2 は次式となる。
| 円錐の切断面の面積:S2 =πx2 | (4) |
上の 2 式を加えると、切断面の和 S は次式となる。
| 円錐の切断面の面積:S=S1+S2 =πr2 | (5) |
上式は x の値にかかわらず S は一定となることを示している。すなわち、半球の断面積と円錐の断面積の和は、半径 r の円の面積となる。これを立体的に考えると、半球の体積と円錐の体積の和は、図 3 右の外側の細線で示される半径 r、高さ r の円柱の体積となる。
| 円柱の体積:πr3 | (6) |
円錐の体積は(積分公式を思い出すと)円柱の体積の 1/3 なので、半球の体積は円柱の体積の残りの 2/3 となる。球の体積は半球の 2 倍なので次式となる。
| 球の体積:2×2/3×πr3 =4/3πr3 | (7) |
球の表面積は、図 1 右のように球を錐体に分割して考える(または上式を r で微分する)と次式となる。
| 球の表面積:4πr2 | (8) |
以上のように、円周を表す π を用いると円の面積、立体の球の表面積や体積も簡単な式で表すことができる。
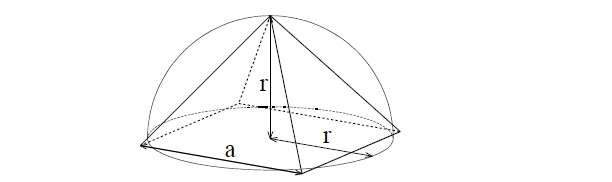
さて、π の値を 3.14 と最初に算出したのは定説では紀元前 3 世紀のアルキメデスである。しかし、それより 2,000 年以上も前に建てられたエジプトのピラミッドに π が用いられているという説がある。最大のクフ王のピラミッドの建設時の高さは 146.7m、底面は正方形で 辺の長さは 230.4m なので、 2× 230.4/146.7= 3.14 とちょうど π の値となる。これは図 4 のように四角錐の底辺の和 4a が半球の円周 π に等しく、高さが r となっていることを示している。このようなことを根拠に「ピラミッドは底辺が赤道を示している地球の北半球を表している」という説がある(反論もある)ことを紹介しておこう 2)。
-
- 参考文献
- 1) 「数学の世界:図形編」、Newton 別冊、2020.4
- 2) グラハム・ハンコック著、大地瞬訳「神々の指紋上下」翔泳社、1996.7
* いしやまゆうじ北海道大学名誉教授
(一社)建築研究振興協会発行「建築の研究」2021.1 原稿