ちょっと真面目チョット皮肉 166
石山祐二*
地震によって 1 階が崩壊する被害はどの地震でもよく見られる（図 1）。この理由は、各階に地震力 P1, P2, P3 が作用すると（図 2）、これらの地震力は下の階に伝達され、下の階ほど大きな力（これを地震層せん断力という）が生じ、1 階で最大となるからである。また、1階は駐車場や店舗として用いられ、耐震壁や筋かいが少なくなり耐震性が低くなることが多いからである。
図 1 地震による 1 階の崩壊（1995 年阪神・淡路大震災）
さらに、地震時の変形が図 2a) のように各階一様となる場合は、地震エネルギーが各階に分散されるが、b)のように 1 階の変形が大きくなる場合は、地震エネルギーは 1 階に集中し、より崩壊し易くなる。
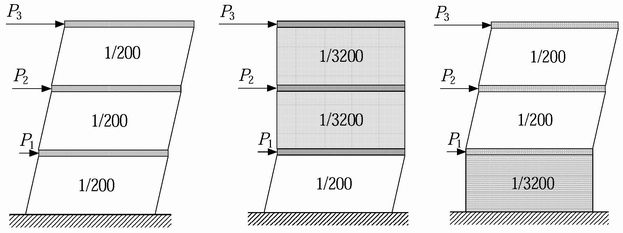a) 各階同一変形 b) 上2 階の変形小 c) 1 階の変形小
図 2 地震力 Pi を受ける各階の変形と層間変形角
建築基準法には、このような被害を防ぐ規定がある。地震力による変形を層間変形角（1/rs）で表し、rs はrsの相加平均とし、各階の剛性率 Rs = rs/rs を計算する。特定の階に変形が集中しないよう Rs≧ 0.6 とし、 Rs < 0.6 の場合は、形状係数 Fs = 2.0 –Rs/0.6 によって、その階の保有水平耐力を割り増しする規定である。
例えば、図 2a) の場合、各階の層間変形角は同一の 1/rs = 1/200 とすると、剛性率は Rs = 1.0、形状係数は Fs = 1.0 となり、割り増しは不要である。図 2b) の場合、上2 階の剛性が高く層間変形角が 1/3200 とすると、剛性率は Rs = 0.17 < 0.6、形状係数は Fs = 1.72 となり、1 階の保有水平耐力を 1.72 倍に割り増しすることになる。この割り増しする値には異論もあろうが、規定としては妥当であろう。
ところが図 2c) の場合、1 階の剛性が高く層間変形角が 1/3200 とすると、上2 階の剛性率は Rs= 0.09 < 0.6、形状係数は Fs = 1.85 となり、上 2 階の保有水平耐力を1.85 倍に割り増しすることになる。一般に、1階の剛性を高くすると、地震時に1 階は地盤と同様に振動するようになるので、上 2 階は 2 階建と同じような挙動をするはずである。それなのに、上 2 階の保有水平耐力を割り増ししなければならない規定には納得できない。
このような問題点は 1981 年に新耐震設計法が施行された直後から指摘されており、2015 年の解説書 1) には剛性率による割り増しを適用しなくともよい場合が示されることになったが、根本的な改正はされていない。
このような問題点が生ずる原因の一つが、層間変形角の逆数 rs の相加平均として rs を求めているからである。すなわち、剛性の低い階の影響を考慮すべきなのに、剛性の高い階が他の階に及ぼす影響を過大に評価していることになっているのである。このため、（層間変形角の逆数 rs ではなく）層間変形角 1/rs とその相加平均との比に応じて剛性率を求める（これは、rs を rsの調和平均として求めることと同じである）のがよいと以前から考えていていて拙著 2) にも書いたことがある。なお a と b の相加平均は (a + b)/2、調和平均は 2/（1/a+1/b）（逆数の相加平均の逆数）である。
地震時の各階の変形から剛性率と形状係数を求めるのは、他国には見られないよい規定ではあるが、実際の地震被害との対応も反映されるように、さらによい規定へと改正されることを望んでいる。
（参考文献） 1) 国土交通省国土技術政策総合研究所、国立研究開発法人建築研究所監修：「2015 年版建築物の構造関係技術基準解説書」、全国官報販売共同組合発行、2015.6
2) 石山祐二：「建築構造を知るための基礎知識 耐震規定と構造動力学」、三和書籍、2008.3.
*いしやまゆうじ 北海道大学名誉教授
（一社）建築研究振興協会発行「建築の研究」2016.6原稿