ちょっと真面目チョット皮肉 152
石山祐二 *
(その 1 )で示したように地震動の加速度応答スペクトルはかなり複雑で、また将来の地震動を予測することは難しいため、設計にはスペクトルを平均し、理想化した図 1 のような設計用加速度応答スペクトルを用いることが多い。
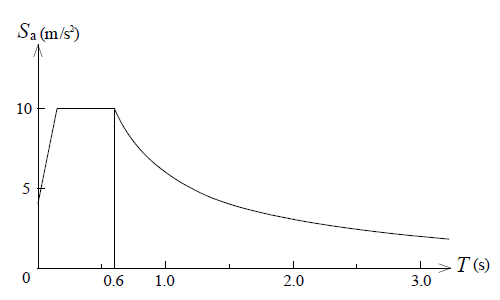
一方、(その 2 )で説明したように、最大応答が固有円振動数 ω の正弦波で表されるとすると、加速度応答 Sa と変位応答 Sd の間には次の関係がある。
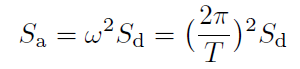 (2)
(2)
ここで、T は構造物の固有周期で T = 2π/ωである。
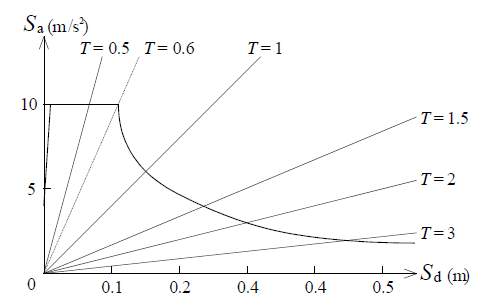
上式より T を一定とすると, Sa と Sd は比例関係にあるので,縦軸を Sa とし横軸を Sd とした図 2 において,原点 O から始まる放射状の直線は,ある一定の T を示すので、図 1 のスペクトを変換すると図 2 となり,これを要求スペクトル(demand spectrum)という。
要求スペクトルは,通常の応答スペクトルに比べて特別な情報を有しているものではないが,構造物の荷重変位曲線は縦軸が荷重,横軸が変位なので,図 3 のように荷重変位曲線と要求スペクトルを重ね合わせて描くことができるという利点がある。なお、図 3 中の破線 a,b,c は,各層の荷重変位曲線を図 4 に示す等価 1 自由度系に縮約した,異なる 3 棟の建築物の荷重変位曲線を示しており,これを耐力スペクトル( capacity spectrum)という。
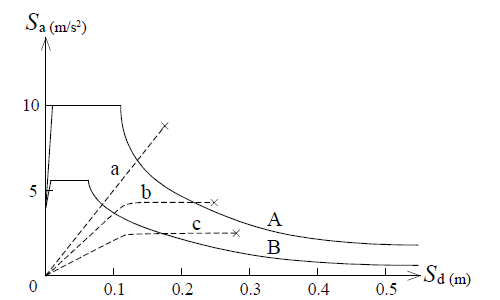
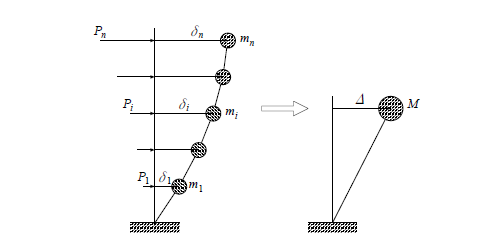
図 3 中の耐力スペクトル a は要求スペクトル A を直線的に横切ってから(×で示される)崩壊に至るので,耐力スペクトル a で表される建築物は,要求スペクトル A で表される地震動に対して弾性限以内の挙動をすることになる。耐力スペクトル b で表される建築物は,塑性領域に入るが要求スペクトル A で表される地震動に耐えることができる。耐力スペクトル c で表される建築物は,要求スペクトル A を横切ることがないので,この地震動に耐えることができない(ただし、塑性領域に入ることによって減衰が増加し、要求スペクトルが低減されるので、耐えることもあり得る)。要求スペクトル B で表される地震動に対しては,耐力スペクトル a, b で表される建築物は弾性限以内で耐えることができ,耐力スペクトル c で表される建築物は塑性領域に入るが耐えることができることになる。
以上のように,地震動の特性を表す要求スペクトルと建築物の特性表す耐力スペクトルを比較し耐震性を検証する手法を「耐力スペクトル法」(Capacity Spectrum Method)といい,日本の限界耐力計算にも取り入れられている。地震動と構造物の耐力を直接比較するこの手法は非常に興味深いが、この手法の妥当性については,地震被害調査を含む今後の調査研究が必要であろう。
(参考文献) Freeman, Sigmund A.,“The Capacity Spectrum Method as a Tool for Seismic Design”, Wissens-management – WM,1998
* いしやまゆうじ 北海道大学名誉教授
(社団法人)建築研究振興協会発行「建築の研究」2013.12 掲載