ちょっと真面目チョット皮肉 150
石山祐二 *
< p style=”text-indent: 1em;”>前回(その 1)で図 1 を示し「 1 階の波形はかなり複雑である。一方、 9階 の最大振幅は 1 階に比べ約 4 倍に増幅され、かつピークが約 1 秒ごとに周期的に表れている。」と書いた。
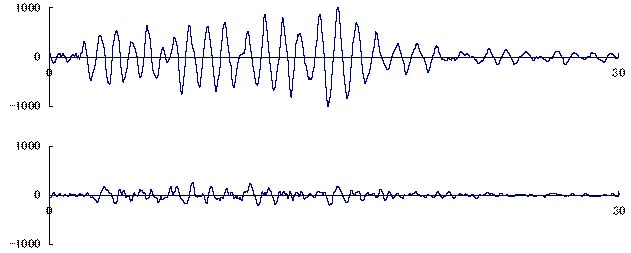
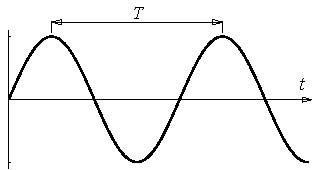
地震動を受けると構造物はいつでもその固有周期 T (図 1 の場合は約 1 秒)で振動するので、応答変位が最大となる時間帯の振動を図 2 のように正弦波で表すと、最大の応答変位 Sd 、固有円振動数 ω( ω =2π/Tの関係がある)として、応答変位 y は次式で表される。
![]()
(1)
上式を時間 t で 1 回微分すると速度、 2 回微分すると加速度が次式のようになる。
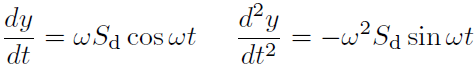
(2)
sin も cos も最大は 1 なので、上式から最大の応答速度 Sv と応答加速度 Sa は次式となる。
![]() (3)
(3)
sin や cos を微分(または積分)する際には、 (2)式から分かるように、 ω を用いる方が簡単なので、数学的には ω を用いることが多いが、工学的には固有周期 T や固有振動数 f =1/T = ω/(2π )を用いることが多い。
いずれにしても、 Sd , Sv , Sa の間には (3)式のような簡単な関係がある。この関係を利用し、図 3 のように横軸に固有周期 T 、縦軸に Sv をいずれも対数目盛で表すと、同図に示されている左右に傾いた目盛から Sa と Sd も読み取ることができる。このような図をトリパータイト応答スペクトルという。
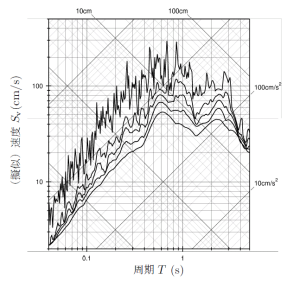
トリパータイト応答スペクトルは、一つの図から応答の加速度も速度も変位も読み取ることができるというメリットの他に、 T =1/f の関係があるので、左右を反転し目盛を逆数(例えば 0.1は 10)にすると横軸が(対数目盛のため)振動数のスペクトルになる。なお、横軸は周期の場合が多いが、振動数の場合もある。
構造物の応答が最大となる時間帯では図 2 のように振幅を正弦波でほぼ表すことができるが、最大の応答変位、速度、加速度を求めると、ここで示した式は厳密には成立しない。このため、上のような式が成立するように求めたものを擬似変位、擬似速度、擬似加速度と表現し、それらを示したものを擬似応答スペクトルという場合もあるが、工学的にはほとんど差異はないので、擬似(pseudo)という表示をしていることはあまりないようである。
(参考文献)石山祐二「耐震規定と構造動力学」三和書籍、2008.3
* いしやまゆうじ 北海道大学名誉教授
(社団法人)建築研究振興協会発行「建築の研究」2013.10 掲載